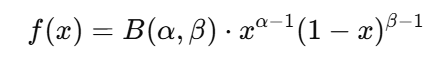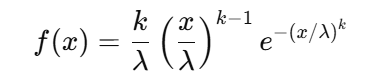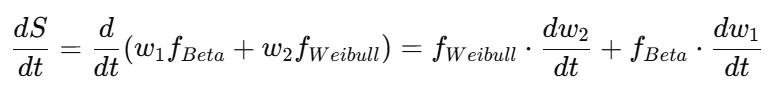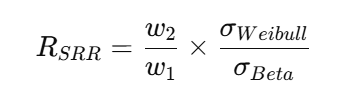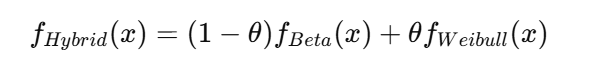現代の製薬業界は、革新的な新薬開発競争の激化と、グローバル市場環境の複雑化に直面しています。企業が持続的な成長を遂げるためには、自社の競争上のポジションを正確に把握し、データに基づいた精緻な戦略を立てることが不可欠です。従来の売上高ランキングや市場シェア分析だけでは見えにくい、業界全体の構造とその中での自社の「立ち位置」を可視化する新たなアプローチとして、「分布構造分析」を活用してみましょう。
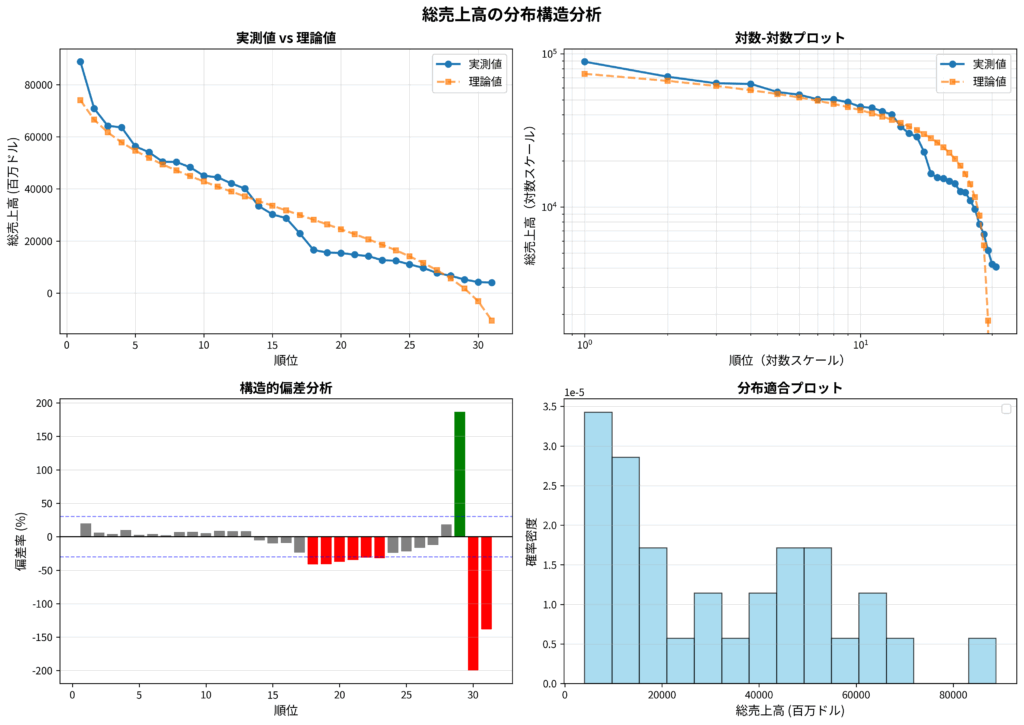
分布構造分析とは、ある集団のデータがどのような法則性に従って構成されているのかを明らかにし、個々の要素がその構造の中でどのような位置にあるのかを定量的に評価する手法です。具体的には、業界全体の売上高などから理論的な期待値を算出し、各企業の実績値がその理論値からどれだけ乖離しているかを分析します。この乖離は、企業が持つ構造的な強みや課題を浮き彫りにします。
世界の製薬市場を俯瞰すると、その売上分布には非常に特徴的な構造が見られます。分析の結果、企業の総売上高は「ガンマ分布」と呼ばれる右裾が長い分布型に従うことが確認されました。これは、少数の大手企業が市場全体の売上を大きく占める一方で、多数の企業が中・下位層に集中する、いわゆる「Winner-Takes-All(勝者総取り)」構造を意味します。
上位にはジョンソン・エンド・ジョンソン、ファイザー、ロシュ、メルクなどの名が並び、これらの企業が市場の主成分を形成しています。一方で、アストラゼネカ、ノボノルディスク、イーライリリーといった中堅勢は、異なる成長軌道を描きながら次の波を形成しており、分布上では第二の山(副構造)を示唆する位置にあります。市場全体を単一のヒエラルキーとして捉えるのではなく、複数の構造層が重なり合う“多層構造的市場”として理解することが重要です。
分析によると、上位5社で市場全体の約35%、上位10社では約60%のシェアを占めており、寡占的な市場構造であることがデータからも裏付けられます。
さらに注目すべきは、各社の「構造的ポジション」です。分析の結果、理論値を大きく上回り卓越したパフォーマンスを示す「成長機会を有する企業群」と、理論値を下回り「効率化の余地を残す企業群」とが明確に分かれました。たとえば、一部の日本企業は、売上規模に対して理論値を上回る利益を上げており、独自の強みを発揮していることが示唆されます。
このような構造は単なる数値の比較にとどまらず、市場の競争原理を映し出す鏡でもあります。ガンマ分布型の市場は、少数のリーダー企業の経営判断が全体の動向に大きな影響を及ぼす「構造的脆弱性」を内包しています。すなわち、一社の戦略転換や不祥事が需給バランスや投資動向を左右しかねないのです。一方で、裾野に位置する企業群には構造的な“成長余地”が眠っており、上位層が成熟・停滞する中で、この裾野をいかに押し上げるかが次の競争の焦点となるでしょう。
製薬産業はしばしば技術革新やパイプラインの強さで語られますが、構造的な視点から見ると、競争力とは単なるR&D投資額の多寡ではなく、市場の中でどの構造層に位置し、どのような分布特性を持つかによって決まります。構造を知ることは、すなわち戦略を立てることに等しいのです。
自社がどの位置に立ち、どの層を狙うべきか──構造の理解こそが、縮小市場で生き残るための最も実践的な経営知といえるでしょう。