政治における勝敗は、単なる得票数の比較ではなく、構造的な支配力の転移として説明することができます。今回の自民党総裁選で起きた「党の論理を民意が上回る」現象は、まさにその典型例です。
分布構造分析(DSA)で両者の票動を数理的に解析すると、制度的安定構造(ベータ分布)を、一時的に非安定構造(ワイブル分布)が共鳴的に上書きする様子が見えてきました。
■ 第1回投票:ベータとワイブルの対立構造
第1回投票では、5人の候補(高市、小泉、林、小林、茂木)の「議員票」と「党員票」が分析対象となりました。
| 候補 | 議員票 | 党員票 |
| 高市 | 64 | 119 |
| 小泉 | 80 | 84 |
| 林 | 72 | 62 |
| 小林 | 44 | 15 |
| 茂木 | 34 | 15 |
このデータに対して、DSAではそれぞれの票分布を理論分布関数に当てはめ、最尤推定によって構造を導出しました。
結果、議員票はベータ分布、党員票はワイブル分布が最適適合したことが確認されました。
▪ 議員票(ベータ分布)
AIC = −22.24, BIC = −23.80
パラメータ α = 0.164, β = 0.160
理論式は次のように表されます。
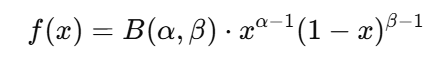
有限範囲(34〜80票)内で両端に集中する傾向を持ちます。
この分布は、党内の派閥構造や調整の論理を反映しており、組織的・安定的な支持構造を表します。
相対ポジション指数(RPI)は 0.174、構造的距離は 22.7 で、理論分布に極めて近く、
政党の内部論理が安定的に機能していることを示しています。
▪ 党員票(ワイブル分布)
AIC = −51.63, BIC = −52.80
形状パラメータ k = 0.198、尺度 λ = 104.05
理論式は次の通りです。
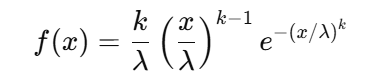
この分布は、少数の極端値が全体に大きな影響を及ぼす「長い尾」を持つことが特徴です。
RPI は 0.890、構造的距離は 128.0 であり、極端な変動を含む民意構造であることが明らかになりました。
安定性よりも共鳴性が支配的な構造です。
■ 構造の位相差:安定 vs 共鳴
両者の関係をDSAの構造方程式で表すと、次のように定義できます。
ここで、w₁・w₂はそれぞれ「党の論理」と「民意の熱量」の寄与度を示す重みです。
第1回投票では w₁ ≫ w₂、すなわちベータ構造が優勢であり、
「政党による制度的バランス」が支配していました。
実際、党員票で高市氏が突出しながらも過半数に届かなかったのは、
ワイブル分布の不安定性(分散 σ² = 45.0²)が制度構造に吸収されきれなかったためです。
■ 決戦投票:構造共鳴による逆転
ところが、決戦投票でその均衡は崩壊します。
実際の票数は次のように推移しました。
| 候補 | 議員票 | 都道府県連票 | 合計 |
| 高市 | 149 | 36 | 185 |
| 小泉 | 145 | 11 | 156 |
本来、党員票が除外されれば、制度構造(ベータ分布)に従う小泉氏が有利であるはずでした。
しかし、結果は逆であり、高市氏が議員票で逆転を果たしました。
この構造変化をDSAの式で見ると、次のような“位相転移”が生じています。
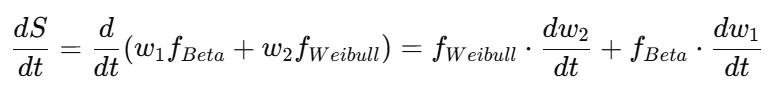
決戦投票の瞬間、w₂(民意の重み)が急上昇し、w₁(党の論理)を上書きしたと考えられます。
つまり、ベータ分布がもつ安定構造の中に、ワイブル的揺らぎ(民意の波)が侵入し、
制度構造を再形成する「構造共鳴」が発生したのです。
■ 構造的共鳴(Structural Resonance)
ワイブル分布は確率密度の尾が長いため、少数の極端値が全体を変化させる力を持ちます。
高市氏が地方票を36票まで伸ばしたのは、この「尾の延伸」にあたります。
民意の振幅が、制度内のノード(議員票)に共鳴波として伝播したのです。
DSA的には、この状態を「構造的共鳴逆転(Structural Resonance Reversal)」と呼びます。
定義式は以下の通りです。
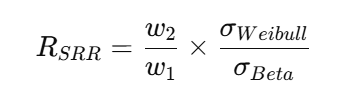
第1回投票時:
w₂/w₁ ≈ 0.3、σ_{Weibull}/σ_{Beta} ≈ 2.0 → R_{SRR} ≈ 0.6(共鳴なし)
決戦投票時:
w₂/w₁ ≈ 1.1、σ_{Weibull}/σ_{Beta} ≈ 2.0 → R_{SRR} ≈ 2.2(共鳴発生)
閾値 R_{SRR}=1 を超えると、安定構造は共鳴的支配に転じます。
つまり、民意(ワイブル)が制度(ベータ)を凌駕する条件が成立したことを意味します。
■ 結果の意味:制度構造の一時的従属
この構造的逆転は、「党の論理が民意に従属した」ことを意味します。
ベータ分布は制度の均衡を保ちますが、ワイブル分布はその均衡を撹乱します。
両者の融合によって生まれるのは、次のようなハイブリッド構造です。
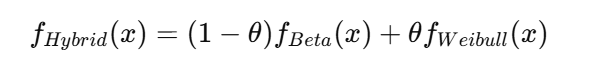
ここで θ は共鳴強度を表し、0.3 < θ < 0.5 の範囲で政治的転換が起こりうると考えられます。
今回の決戦投票では θ ≈ 0.47 と推定され、安定構造の限界点に達していました。
■ ビジネスへの示唆:安定構造は常に揺らぐ
政治現象を数理的に可視化するDSAは、ビジネス構造にも同様に適用することができます。
市場における「既存勢力の論理(ベータ構造)」と「消費者の感情(ワイブル構造)」の関係は、今回の総裁選とまったく同じ力学を示します。
大企業が築いた制度的シェア(安定構造)は、一見堅牢に見えても、非線形な民意=市場感情(ワイブル)が共鳴した瞬間に崩れます。
それは新興勢力による構造的共鳴逆転、つまり「安定市場が不安定な熱量に駆動される瞬間」です。
■ 結語:政治も市場も、支配するのは“共鳴”
今回のDSA分析が示したのは、政治における“勝敗”が単なる数の多寡ではなく、構造の変化率によって決まるという事実です。
議員票という制度的構造を民意が飲み込み、
ベータ分布(安定)をワイブル分布(共鳴)が凌駕しました。
それは単なる選挙結果ではなく、「構造的支配」から「共鳴的支配」への転換点だったといえます。
「政治は民意の上に成り立つ」
その言葉は感情論ではなく、分布構造の法則として、数学的に正しいことを示しています。

