政治の世界では「運」や「風向き」といった言葉で結果を語られることが多いですが、データ構造の視点から見ると、勝敗には明確なパターンが存在します。今回の自民党総裁選で高市早苗氏が勝利した背景には、まさにその“構造的必然”がありました。分布構造分析によって明らかになったのは、民意と党の論理の交錯点に立つ高市氏の「構造的優位性」でした。
■ 民意が党の論理を上回るとき、構造は高市氏を選んだ
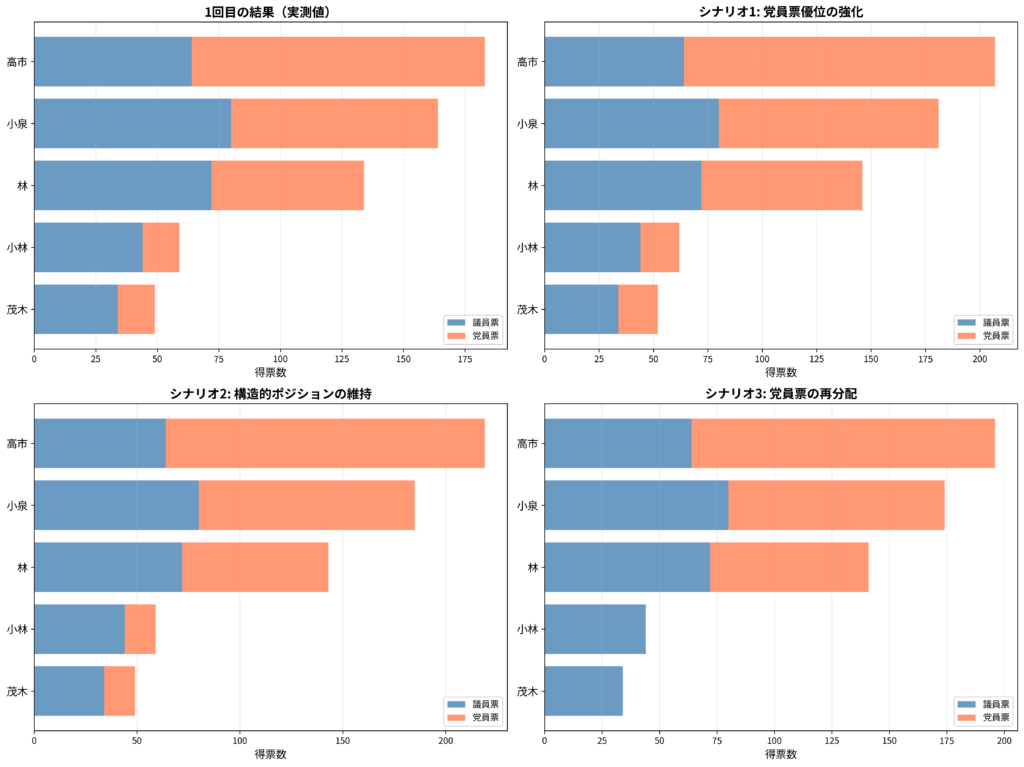
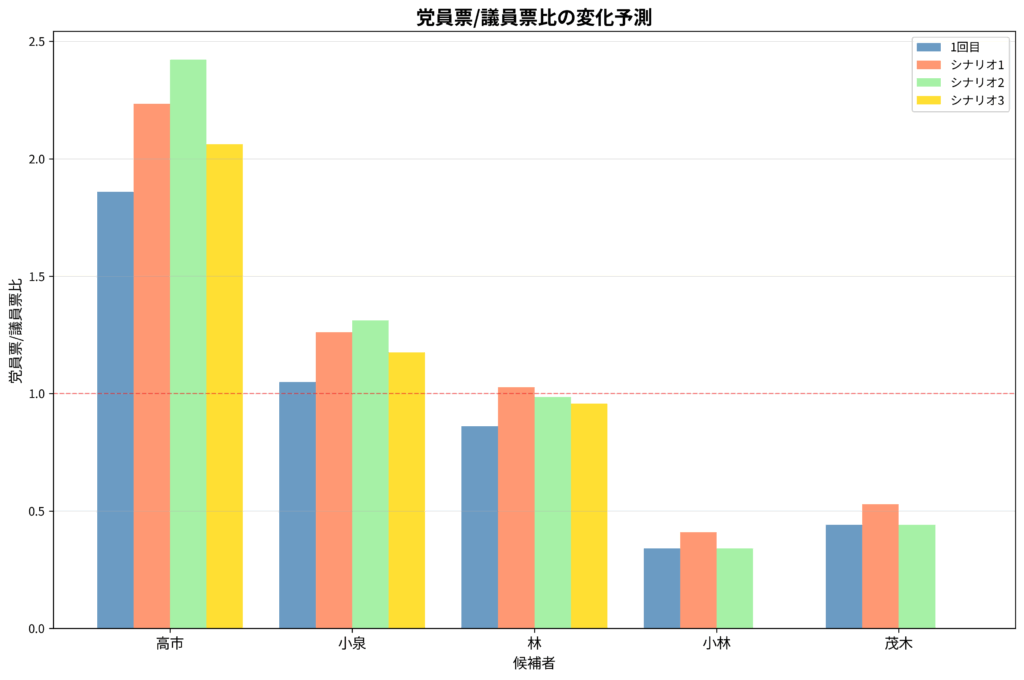
高市氏は5名の候補の中で唯一、党員票の比率が圧倒的に高い候補でした。党員票119票に対し、議員票64票。比率にして1.86倍と、2位の小泉進次郎氏(1.05倍)を大きく引き離す構造を持っていました。
つまり、「党の論理」よりも「民意」が重視される条件下では、最初から高市氏が最も勝ちやすい構造にあったということです。
分布構造分析による予測分析では、複数のシナリオを想定しても高市氏がすべてで1位を維持し、得票予測は196~219票と安定的でした。小泉氏との差は26~34票に及び、構造上の優位性がそのまま選挙結果として具現化した形です。
■ 支持構造の「一貫性」と「広がり」
もう一つ注目すべきは、議員票と党員票の相関係数0.756という高い整合性です。
これは、議員からの支持を一定程度確保しつつ、党員(すなわち民意)から圧倒的な支持を受けていたことを示しています。高市氏は特定の派閥に依存するのではなく、民意を媒介とした“支持のネットワーク構造”を形成していたのです。
この点こそが「勝つべくして勝った」理由だといえます。単に票を積み上げたのではなく、構造的に最も有利なポジションを占めていたのです。
■ 数字が示す「必然」のメカニズム
分布構造分析は単なる統計的予測ではありません。分布の形状とその安定性をもとに、どの要素が勝敗を決定づけるかを明らかにします。今回の分析によると、次のような特徴が見られました。
- 議員票:高い予測可能性(ベータ分布、RPI 0.174)
- 党員票:中~低の予測可能性(ワイブル分布、RPI 0.890)
- 最終順位:高い安定性(全シナリオで変動なし)
これらの結果は、民意という不確定要素の中でも、高市氏の支持構造が最も「ゆらぎにくい」ものであったことを示しています。
■ データ構造から見える「政治の必然」
政治はしばしば“空気”や“勢い”に左右されると考えられがちですが、分布構造分析の視点から見ると、その背後にも明確な構造的ロジックが存在します。
高市氏の勝利は偶然ではなく、民意と党内力学の結節点を先取りした構造的ポジショニングの勝利だったといえます。
選挙とは、理念や政策だけでなく、支持の「構造」をどのように設計できるかという戦いでもあります。
これはビジネスの世界にも通じます。どんなに優れた製品や戦略を持っていても、市場構造に対して不利なポジションにある限り、勝つことは難しいのです。
高市氏の勝因は、政治の世界における“構造的戦略”の重要性を改めて示す事例であり、データが示す「必然の勝利」だったといえるでしょう。